CNOT Algorithm

System-Only CNOT Algorithm

The CNOTAlgorithm is used to generate quantum circuits that implement the exponentials of PauliProducts. It assumes full connectivity between the qubits, or at least that a CNOT gate is natively available on each pair of qubits. For each term in the PauliProduct, the following operations are applied:

• The appropriate basis rotation is applied to transform it to the Pauli $Z$ basis
• A sequence of CNOT gates is applied between each qubits that appear in the Pauli string
• A RotateZ is applied to the last qubit in the PauliProduct
• The sequence of CNOTs is applied in reverse
• The basis rotations are undone

For example, the CNOT decomposition for the term $e^{i\frac{\theta }{2}{Z}_0{Z}_1}$ is given by the following circuit

and similarly for $e^{i\frac{\theta }{2}{Z}_0{Z}_1{Z}_2}$

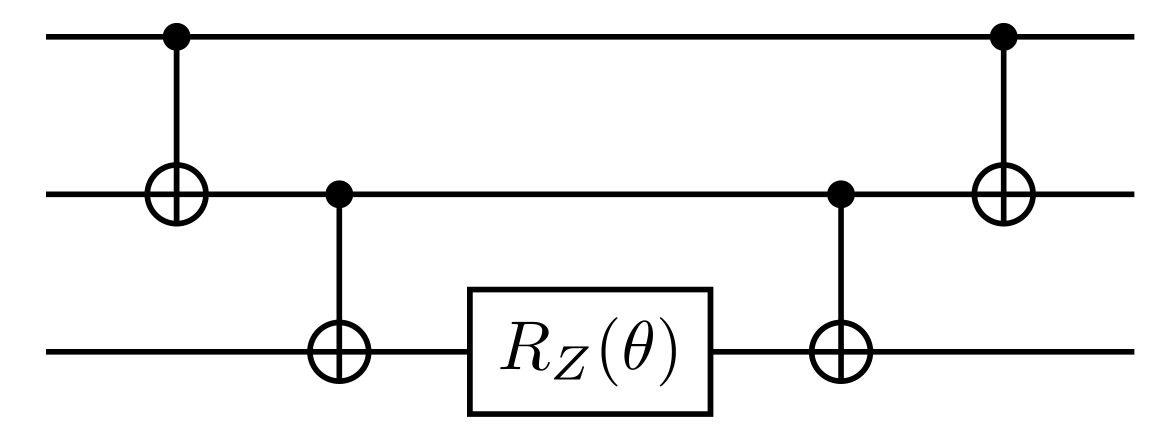
For the term $e^{i\frac{\theta }{2}{X}_0{X}_1}=H_0{H}_1{e}^{i\frac{\theta }{2}{Z}_0{Z}_1}{H}_0{H}_1$ we need basis rotations with Hadamard gates

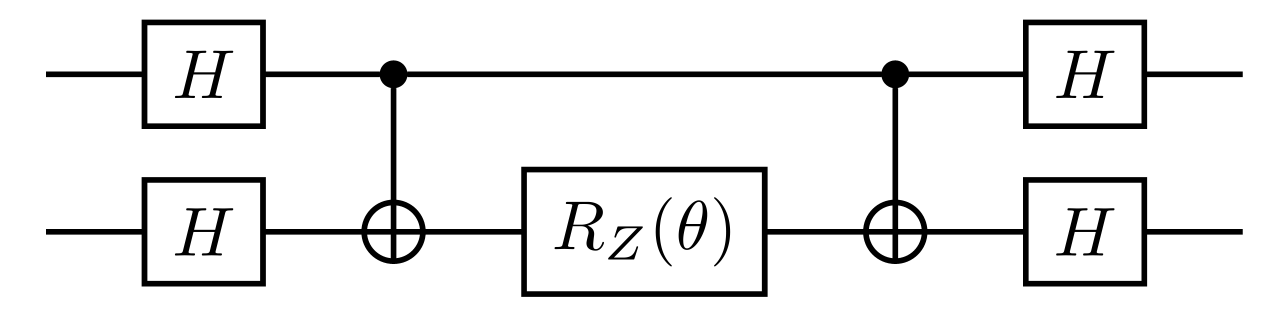
System-Bath CNOT Algorithm

The SystemBathCNOTAlgorithm generalizes the CNOTAlgorithm to the case of a spin system coupled to a spin bath.

The use_bath_as_control boolean flag is used to decide which one between the system qubit and the bath qubit involved in a two-qubit interaction term should be the control, and which should be the target, and therefore also on which of the two the single qubit rotation is applied.

All system-only or bath-only terms are implemented using the CNOTAlgorithm, while the two-qubit interaction terms between system and bath are implemented with the following logic:

• If the bath operator is Pauli $X$, then the system basis is rotated to the Pauli $X$ basis, and CNOTs are added as in the CNOTAlgorithm, with the single-qubit rotation involved being RotateX (applied on the bath qubit or the system qubit depending on use_bath_as_control).
• If the bath operator is not Pauli $X$, the same logic as the CNOTAlgorithm is used, again with use_bath_as_control deciding on which qubit the RotateZ is applied.